木
親子関係を持ったデータ構造。木の形をしている。
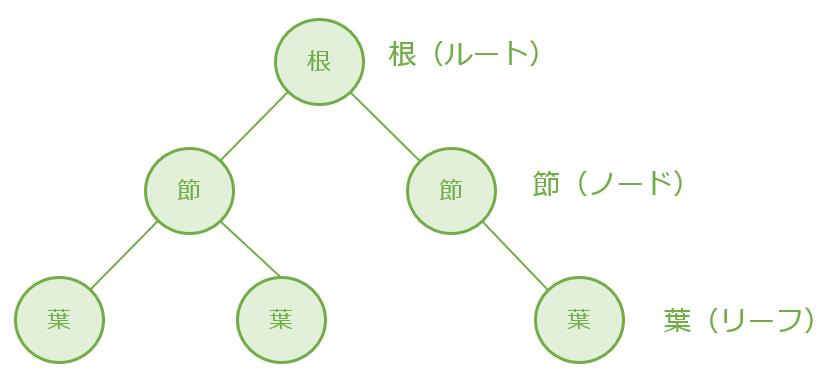
木構造は、節の集まりであり、最上位に位置する節を根(ルート)、最下位に位置する節を葉(リーフ)といいう。
1個上の節を「親」、1個下の節を「子」として考える。
木構造は、2分木と多分木で分類することができる。
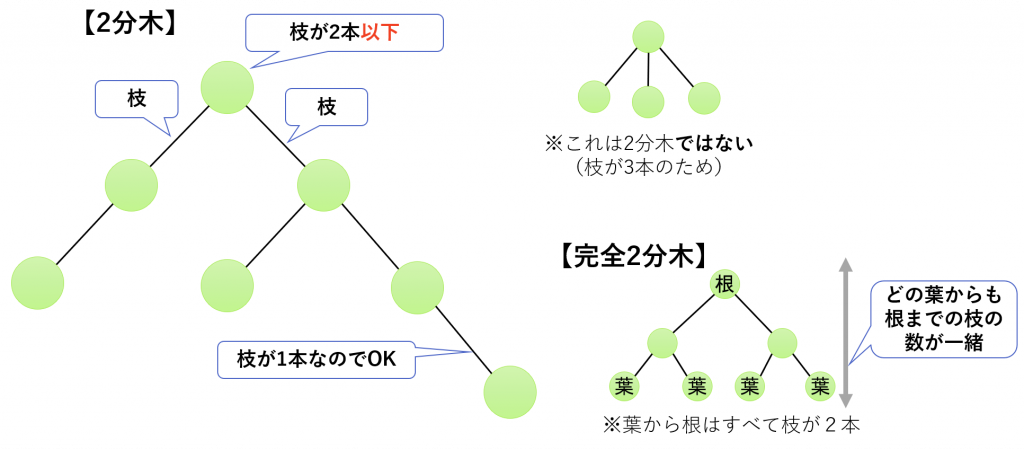
2分木
一般的な2分木 → 子が0~2個である。
完全2分木 → 葉以外の節で子が必ず2個である。
多分木
子が3個以上である。上の画像の2分木でないほう。
2分探索木
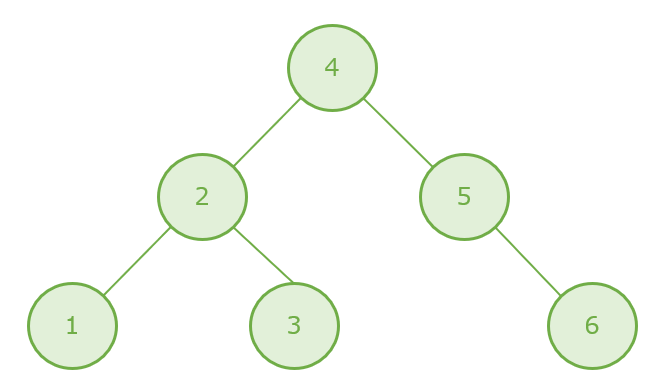
2分木の各ノードにデータをもたせることで探索を行えるようにした木
左部分と右部分の関係が「左の子 < 親 < 右の子」になっているのが特徴である。
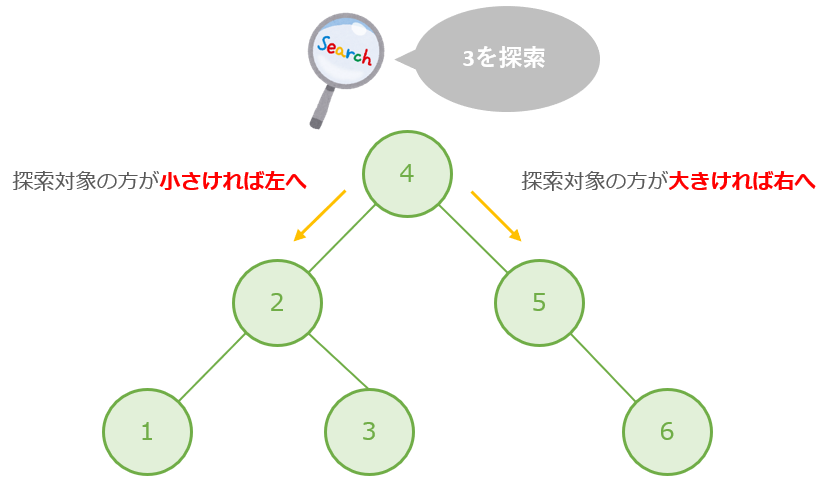
探索したいデータを3としたとき、探索する過程は
3<4 → 3>2 → 3=3 で3が見つかった!
追加したいデータを7としたとき、データを「大小で分けている」ため、データをたどって、データの追加も容易である。
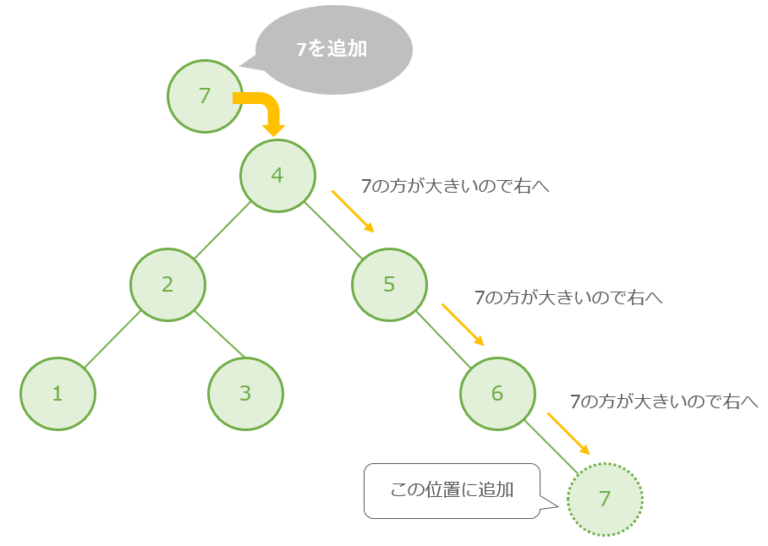
理想的な2分探索木は、完全2分木
最悪な2分探索木は、子が1個のまま、ずっと続いている木
木の巡回
訪問順序によって幅優先巡回と深さ優先巡回に分かれる。
幅優先巡回
深さは、ルートを0として数えていく。
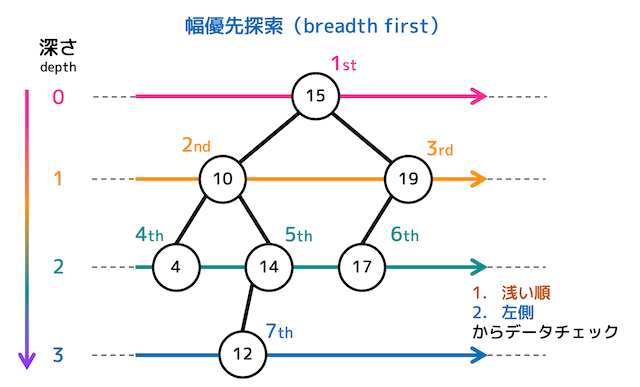
深さ優先巡回
3つの方法に分かれて巡回することができる。形で覚えることをおすすめする。
- 行きがけ(先行順)
- 通りがけ(中間順)
- 帰りがけ(後行順)
行きがけ(先行順)
{15,10,4,14,12,19,17}として取り出すことができる。
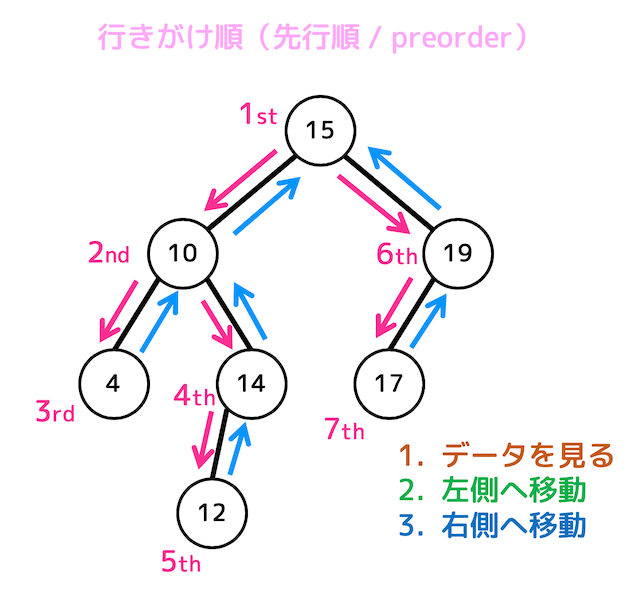
通りがけ(中間順)
{4,10,12,14,15,17,19}として取り出すことができる。
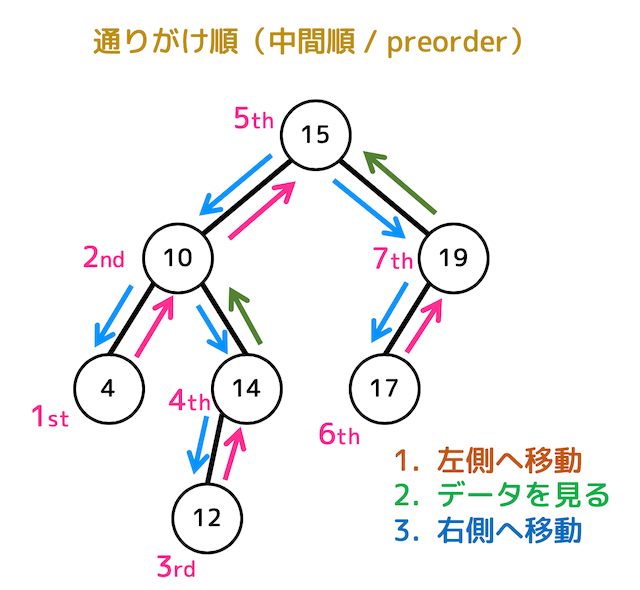
帰りがけ(後行順)
{4,12,14,10,17,19,15}として取り出すことができる。
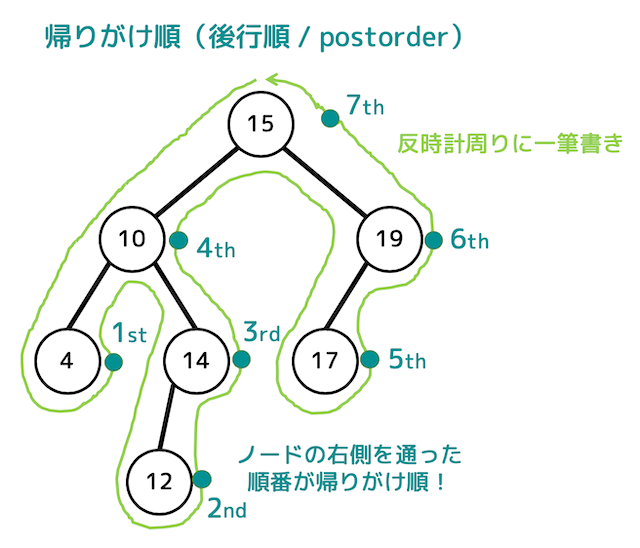
手でなぞってみて、大体のイメージをつかむことが大事
ヒープ
ヒープの条件は2つある。
- 「親 > 子」などの一定の大小関係が成立している。
よって、「親 > 子」の場合は、必ずルートは最大値である。 - 完全2分木である。
ヒープは、幅優先巡回によって配列に表すことができる。
このとき、親の添え字を「i」としたとき、左の子は「2i + 1」右の子は「2i + 2」となる。
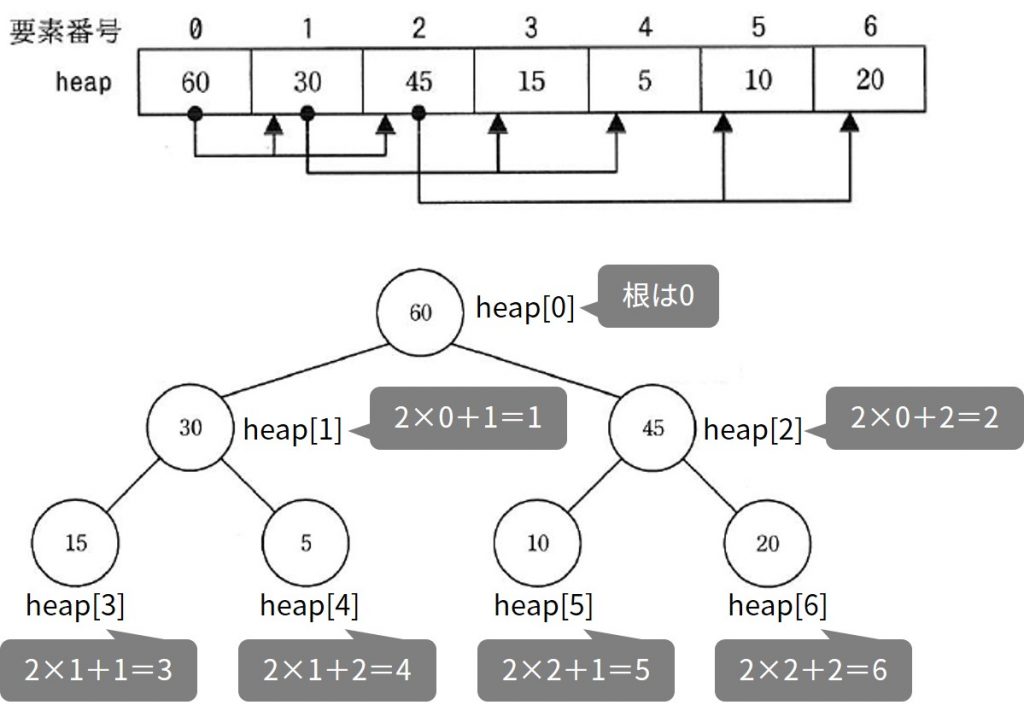
ヒープはデータを整列させるときに使う。(ヒープソート)
仕組みはルートに最大値または最小値があるため、それを他の配列に格納したり確定させたりして、残ったデータでまたヒープを作ってを繰り返していく。
ヒープのアルゴリズムの仕組みを知りたい人は、基本情報技術者過去問題 平成30年春期 午後問8(データ構造及びアルゴリズム)|基本情報技術者試験.com (fe-siken.com)の設問1を解いてみてください。再帰的処理という「処理の中に同じ処理を入れる」ので考えるのが複雑になりますが、自分なりのイメージを見つけて考えてください。
B木
バランス多分木ともいい、枝が複数ある木構造のうち、根からすべての葉の深さが同じで、枝が一方向に偏らない。よって、計算量が莫大になることがない(安定している)から、探索用のデータ構造としてよく使われる。
- 葉ノード以外はすべて2つ以上の子ノードを持つ
- M個のキーを持つ節点はM+1個の子ノードを持つ
- 葉ノードはすべて同じレベル(深さ)になる
- 子ノードには小さい値と大きい値が入り、親ノードには中間値が入る構造になる
条件がいろいろ書いてあるが基本情報では詳しく触れないため、「こんなイメージの多分木なんだー」ぐらいでよい。