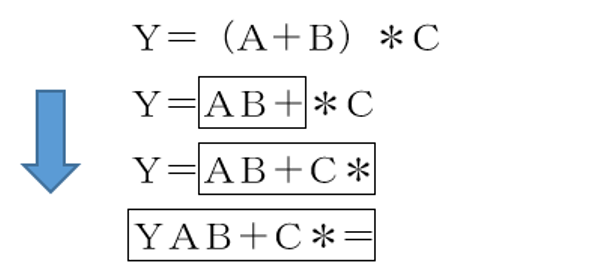どれもよく出てくるのでしっかりと問題とともに理解することが大事
BNF
バッカス記法。プログラムの文法を定義するために導入された記入法
| 記号 | 意味 |
|---|---|
| <記号> | 置き換え可能である(非終端記号)ことをあらわす |
| ::= | 「左辺は右辺である」という意味をあらわす |
| | | 「または」という意味をあらわす |
<数字> :: = 1 | 2 | 3
<英字> :: = A | B | C
<英数字> :: = <英字><数字>
上記の例では<数字>は「1」または「2」または「3」、<英字>は「A」または「B」または「C」、<英数字>は <英字><数字>であるということをあらわしている。
よって、上記の定義下では「1A」は英数字とはならない。
再帰的定義
<数字> :: = 1 | 2 | 3
<英字> :: = A | B | C
<英数字> :: = <英字>|<英数字><数字>
BNF記法では定義の中に自分自身を含むことができます。このような手法を再帰的定義という。
この場合英数字と定義できるものは、<英字>から始まりそのあとはすべて<数字>である文字である。
例:A、A111など
オートマトン
計算機が入力に対してどのように動作するかという仕組みを数学的に表現したモデル
各入力に対して動作が一意に定まる有限オートマトンがよく使われる。
有限オートマトンでは状態遷移図が使われる。
| 名称 | 記号 | 説明 |
|---|---|---|
| 状態 | 状態をあらわす | |
| 受理状態 | 受理状態をあらわす | |
| 遷移 | 遷移をあらわす |
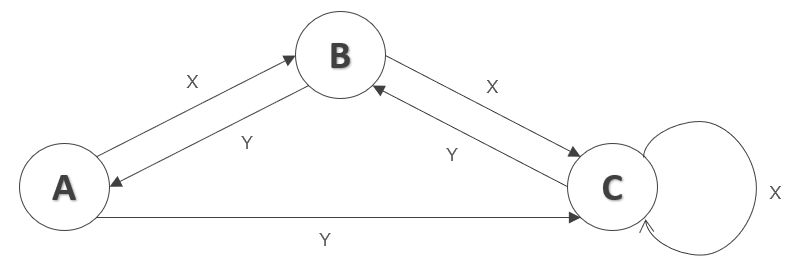
例題
次の状態遷移図で表現されるオートマトンで受理されるビット列はどれか。
ア.00100
イ.10110
ウ.11110
エ.00111
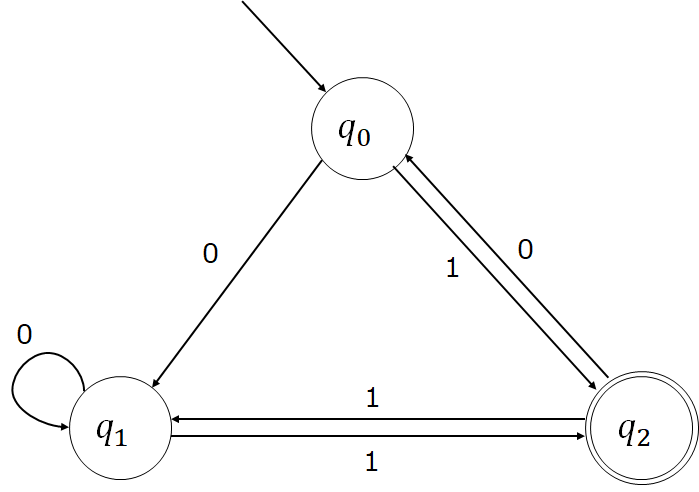
q2の受理状態で終わるためには、最後が「1」でなければならないため、答えは「エ」となる。
逆ポーランド記法
通常は、9 + 3 のように「項 演算子 項」となるが、逆ポーランド記法では、39+ のように「項 項 演算子」の順番で記述する。(コンピュータの演算の仕組みに合わせて)
その仕組みについては、スタックを用いた仕組みであり、後ほど出てくる。