用語チェック
集合 → ある特性の性質をもった集まり。
全体集合 → 対象条件そのもの。UまたはΩと表す。
空集合 → 要素を持たない集合。∅と表す。
部分集合 → ある集合の一部分で構成されている集合。
ベン図 → 円や四角などを用いて、視覚的に集合の関係を表す図。
集合
集合の表記は以下の通りである。
- 要素を 1 つ 1 つ書き並べる場合
A={a,b,c,⋯} - 要素の満たす条件を示す場合
A={x∣条件} - 集合 A に含まれる要素の個数は n(A)
例として、集合Aを16の正の約数とするとき
- 要素を 1 つ 1 つ書き並べる場合
A={1,2,4,8,16} - 要素の満たす条件を示す場合
A={x∣x は 16 の正の約数}
要素の個数は、n(A)=5
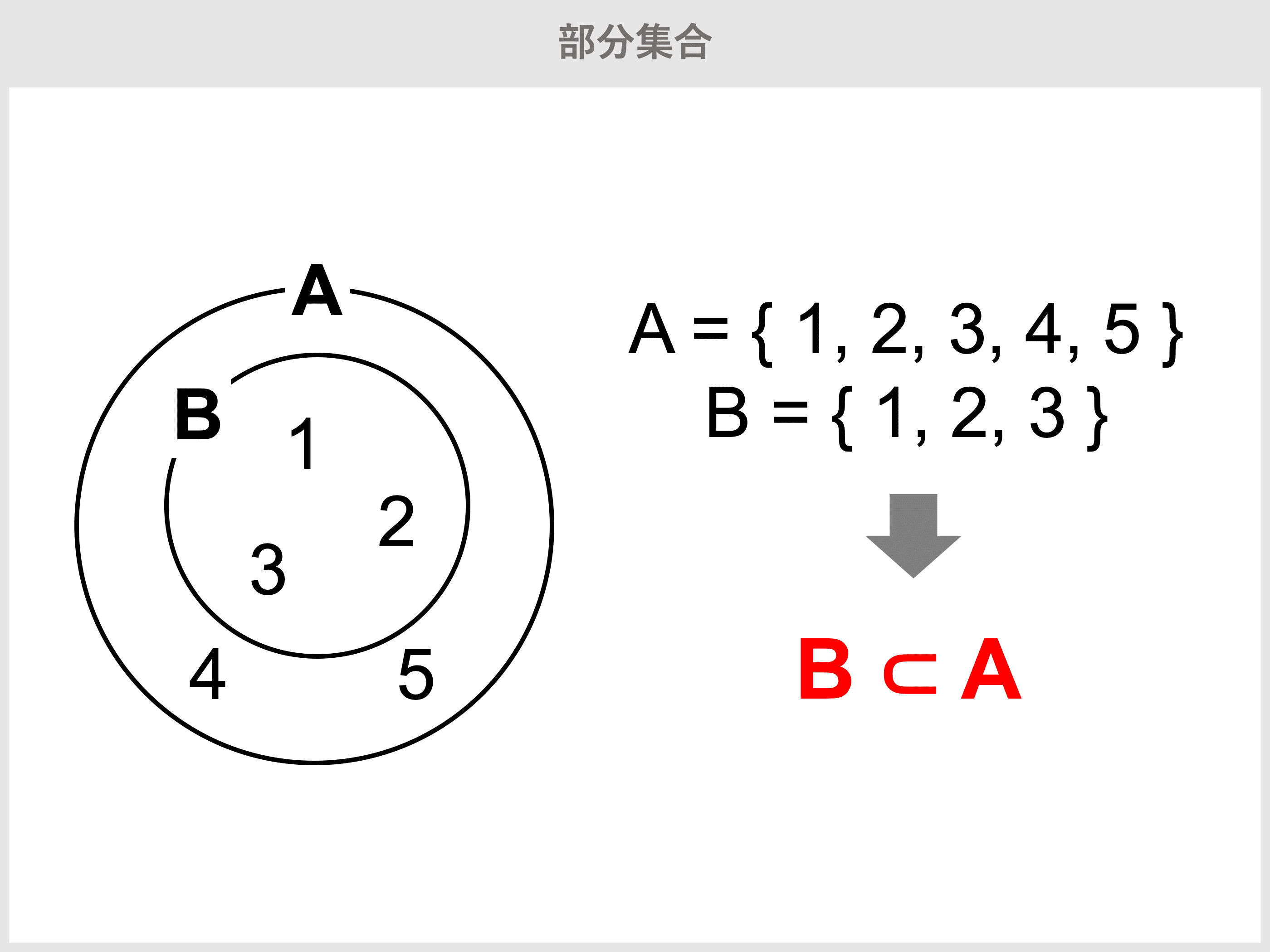
部分集合
この写真の場合、BはAの部分集合であるといえる。
ベン図
集合を表すときは、ベン図をよく用いる。
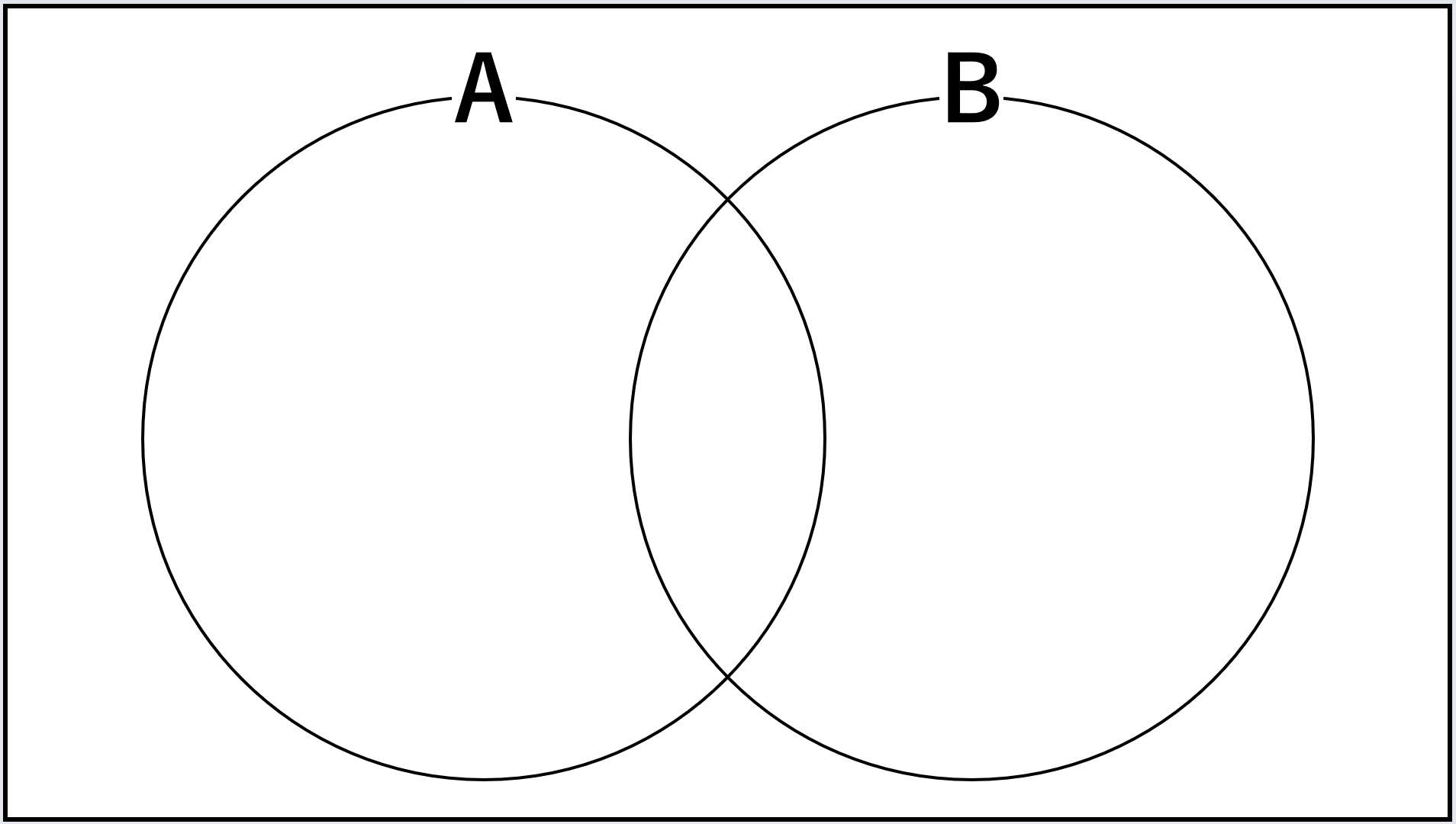
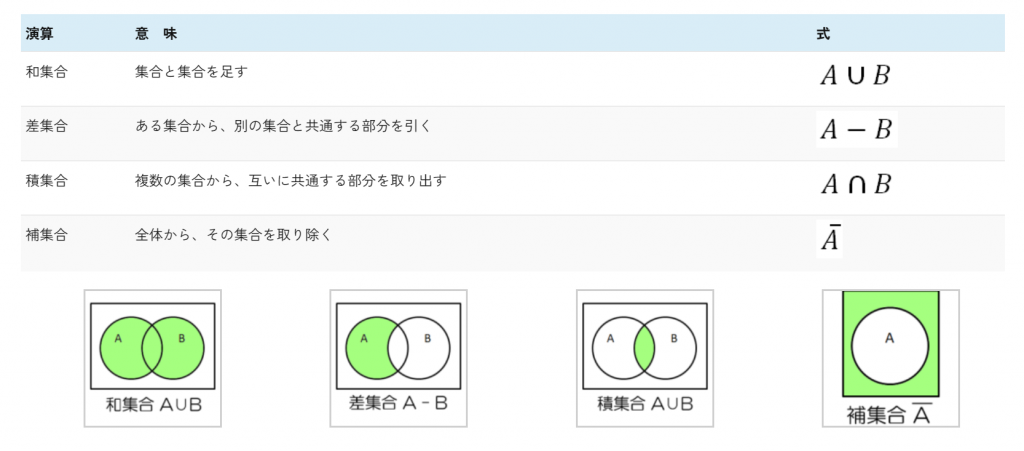
集合を表すときには4つの演算子(記号)がある。
下記のベン図を見るとわかりやすい。
集合に関する有名な法則
ド・モルガンの法則
がある。

でもこれは、ベン図で考えるとほんとに当たり前の法則であり、問題を解くときに効率よく考えるために覚えておくのがとよい。