用語チェック
2進数 → 0,1の『2』種類の数字からなる数値(コンピュータが使用する)
10進数 → 0,1,2,3,4,5,6,7,8,9の『10』種類の数字からなる数値(私たちが使用する)
基数 → 数字に何種類の文字を使用しているか(10進数の基数は10)
ビット → 2進数の桁、情報の最小単位(0か1か)
バイト → 8ビット(空の枠が8個あるイメージ)
2進数から10進数に基数変換
基数を変換することを『基数変換』
10進数は桁ごとに1の桁、10の桁、100の桁・・・があり、
これは桁ごとに基数倍していることがわかる。
| 桁数 | 4 | 3 | 2 | 1 |
| 桁ごとの数字 | 103 =1000 | 102 =100 | 101 =10 | 100 =1 |
| 例の数 | 1 | 0 | 1 | 1 |
今回は 1000+10+1 = 1011 となる。
上記と同じように2進数でも桁ごと数字があり、それは次のように表す。
| ビット数(桁数) | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 |
| 桁ごとの数字(重み) | 27 =128 | 26 =64 | 25 =32 | 24 =16 | 23 =8 | 22 =4 | 21 =2 | 20 =1 |
| 例の数 | 1 | 0 | 1 | 1 | 0 | 0 | 0 | 1 |
今回は 128+32+16+1 = 177 となる。
よって、(10110001)2 = (177)10
練習問題 次の2進数を10進数に直しなさい。
(1) 1000010
(2) 01110111
(3) 11101110
答え:66,119,238
10進数から2進数に基数変換
二つの方法がある。
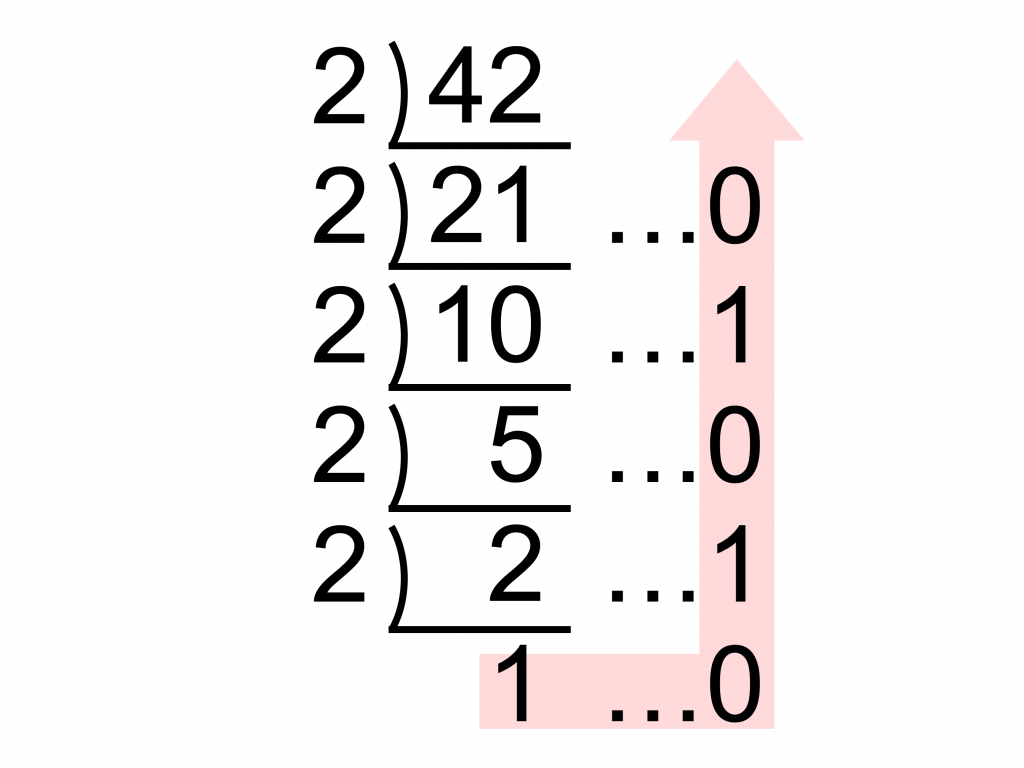
例として(42)10を2進数に変換する。
一つ目の方法 2のべき乗に分解して考える
| ビット数 | 6 | 5 | 4 | 3 | 2 | 1 |
| 重み | 32 | 16 | 8 | 4 | 2 | 1 |
| 42 | 1 | 0 | 1 | 0 | 1 | 0 |
42-32 = 10 → 10 – 8 = 2 → 2 – 2 = 0
101010
2つ目の方法 2で何回割れるか
元の数を2で割っていくことを反復することで求めることもできる。
これは2で割った時の余りは0,1のみであることを活かした方法であり、この場合の最後の1は2を5回割っていることを示し、25を背負っているとイメージ。
101010
練習問題 次の10進数を2進数に直しなさい。
(1) 66
(2) 119
(3) 238
答え:1000010,01110111,11101110
2進数の加減算、乗除算
10進数と同じよう桁上げと桁借りを行う。
加算
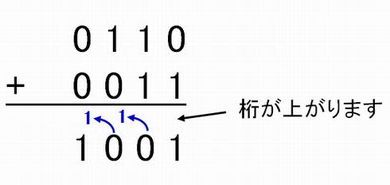
10進数の 9 + 6 = 15 では桁上げが生じている。
同様に2進数での 0110 + 0011 は次のようになる。
減算
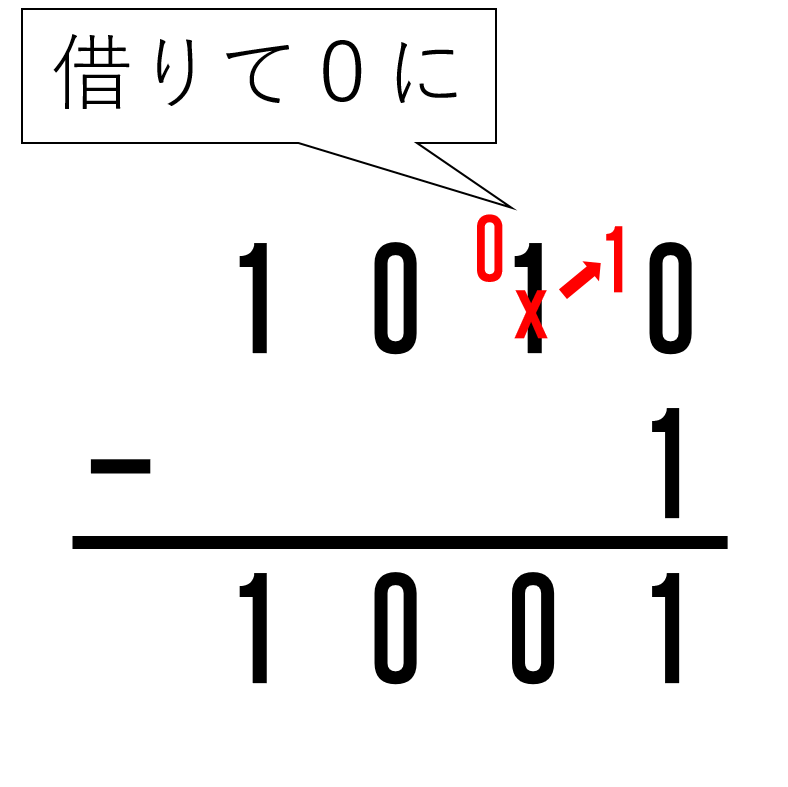
10進数の 15 – 9 = 7では桁借りが生じている。
同様に2進数での 1010 – 1 は次のようになる。
乗算
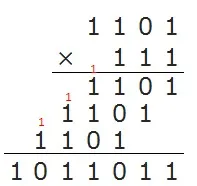
10進数と同じように筆算を行うことができる。
加算で行った桁上げを使う。
徐算
10進数と同じように筆算を行うことができる。
減算で行った桁借りを使う。
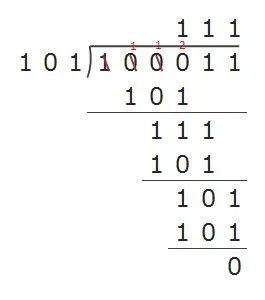
練習問題 次の2進数を計算しなさい。
(1) 10010+11011
(2) 101-11
(3) 111*1010
(4) 10001/101
答え:101101, 10, 1000110, 11あまり10
2進小数と変換
10進数での小数点が1/10倍していくように2進数では1/2倍していく。
2進小数から10進小数
| ビット数(桁数) | 0 | -1 | -2 | -3 | -4 |
| 桁ごとの数字(重み) | 20 | 2-1 =1/2 | 2-2 =1/4 | 2-3 =1/8 | 2-4 =1/16 |
| 例の数 | 0. | 1 | 0 | 1 | 1 |
(0.1011)2 = 0.5+0.125+0.0625 = (0.6875)10
10進小数から2進小数
2つの方法がある。
例として(0.625)10を変換する。
一つ目の方法 2のべき乗に分解して考える
| ビット数(桁数) | 0 | -1 | -2 | -3 | -4 |
| 桁ごとの数字(重み) | 20 | 2-1 =1/2 | 2-2 =1/4 | 2-3 =1/8 | 2-4 =1/16 |
| 0.625 | 0. | 1 | 0 | 1 | 0 |
0.625-0.5 = 0.125 → 0.125-0.125 = 0
2つ目の方法 2でかけてみる
小数点以下の10進数に2を掛けた結果の小数部分が「0」になるまで掛けていき変換する。
2を1回かけて1になるのは0.5
2を3回かけて1になるのは0.125のようなイメージ
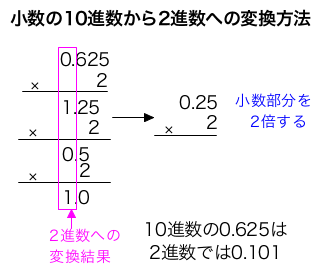
注意 2進小数では表せない数は循環し、その過程で誤差が生じることがある。
練習問題 2進小数を10進小数、10進小数を2進小数に変換しなさい。
(1) (0.1111)2
(2) (0.0625)10
(3) (1.7)10
答え:(0.9375)10, (0.0001)2, 約(1.10110011)2