用語チェック
固定小数点数 → ある限られた範囲内で小数点が特定の位置に固定されている。
浮動小数点数 → 「符号」「指数部」「仮数部」の形式で表現して、広い範囲の実数を表現できる。
正規化 → 浮動小数点数において、小数点の位置を調整し最上位桁を0以外の値にする作業
IEEE → アイトリプルイー:米国電気電子技術者協会(そういう団体があるんだって思うといい。)
誤差 →
| 丸め誤差 | 限られた桁数まで計算して残りを切上げや切下げする事で生じる誤差。 |
| 打ち切り誤差 | 終わらない計算を打ち切ることによる誤差。 |
| 桁落ち | 大きな桁数かつ似ている数字の、差を求めた時に起こる誤差。有効桁数が大きく減ってしまうこと。 |
| 情報落ち | 絶対値の大きな数と、絶対値の小さな数を加算したり減算したりするとき一部の桁しか反映されない誤差。 |
| 桁あふれ誤差 | 表現範囲を超えてしまう誤差。(アンダーフロー、オーバフロー) |
下で詳しく説明する。
固定小数点と浮動小数点
固定小数点
小数点を固定して表現する。
整数を扱う場合が多く、その場合は小数点は一番最後におく。
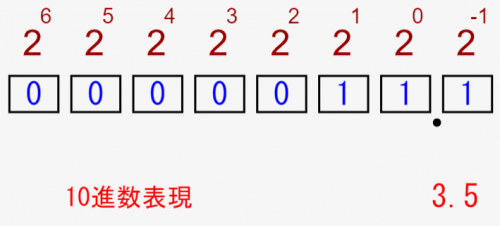
浮動小数点
このように分けて小数部を含んだ広い範囲を表現できる。基本的には(符号)仮数*基数指数の形式で数を表現する。
(IEEE754形式)では仮数を「1.・・・」となるように正規化するため、式にすると(1+仮数部)となる。
指数部には補数表現(負の数を表現する)方法は使わず、最初から+127にしておいて、実際には「指数部-127」で表現する。
式にすると、(符号) * (1 + 仮数部) * 2指数部-127


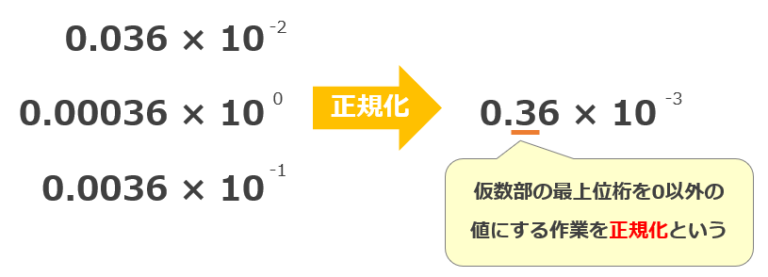
正規化
浮動小数点数において、小数点の位置を調整し最上位桁を0以外の値にする操作
様々な表現を一意にし、有効数字の桁数を確保するため。
誤差
| 丸め誤差 | 限られた桁数で計算して切上げや切下げ、四捨五入することでで生じる誤差。 |
| 打ち切り誤差 | 終わらない計算を打ち切ることによる誤差。 |
| 桁落ち | 大きな桁数かつ似ている数字の、差を求めた時に起こる誤差。有効桁数が大きく減ってしまうこと。 |
| 情報落ち | 絶対値の大きな数と、絶対値の小さな数を加算したり減算したりするとき一部の桁しか反映されない誤差。 |
| 桁あふれ誤差 | 表現範囲を超えてしまう誤差。(アンダーフロー、オーバフロー) |
丸め誤差
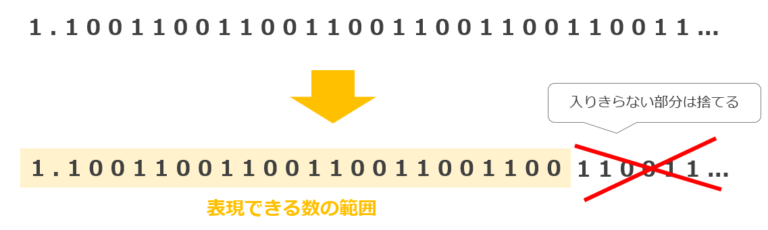
切捨て、切上げ、四捨五入で丸めたイメージ
打ち切り誤差

無限だから打ち切ったイメージ
情報落ち

大小の差があって無視されるイメージ
桁落ち

有効桁(信頼できる桁)が減って困るイメージ
桁あふれ誤差
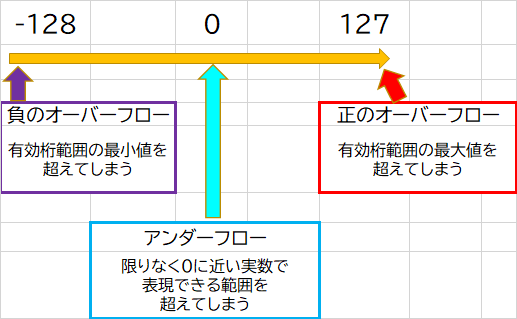
大きすぎもしくは小さすぎで表現できないイメージ
似てる表現が多いですが、明確に分けることなく、「こういうイメージなんだ」、「こういうキーワードがあればいいんだ」など軽く分けて理解しておくことが大事です。