代表値
データの集まりあった時、その集まりの代表となる値を代表値という。
3つの代表値があり、特徴を理解して使い分ける必要がある。
| 平均値 | データの総和/データの件数 |
| 中央値(メジアン) | データを整列させたとき、中央に位置する値 |
| 最頻値(モード) | 一番出てくる値(度数が大きい値) |
平均値
データの総和/データの件数で求まる値 であるため、極端な値の影響を強く受ける。
| おすすめ | 段階評価のアンケート、テストの点数、ある程度の数字範囲に収まるデータなど |
| あまりおすすめしない | ばらつきや個人差が出やすいデータ |
中央値
数値を小さい方または大きい方から順に並べたときに、真ん中に位置する値 であるため、極端な値の影響を受けないが、全体を把握することが難しい。
| おすすめ | ばらつきや個人差が出やすいデータ |
| あまりおすすめしない | 比較データ(前年度比較など) |
最頻値
一番個数が多い値 であるため、極端な値の影響を受けないが、データが少ないと無意味な値となることがある。
| おすすめ | データ数が多いデータやばらつきや個人差が出やすいデータ |
| あまりおすすめしない | データ数が少ないデータ |
データのばらつき
分散や標準偏差で表す。
分散と標準偏差ともに「データの平均値からの散らばり具合を表す指標」であるが、
分散はただ散らばりを表すだけであり、標準偏差は平均値とともに散らばり具体的にみると考えるとよい。
分散
大きいとばらつきが多い。小さいとばらつきが少ない。

標準偏差
分散は偏差(その値と平均との差)を2乗しているため、それをもとに戻す操作(√をかける)をすると平均値とともに具体的なばらつきを見ることができる。

標準偏差10と標準偏差20の例:
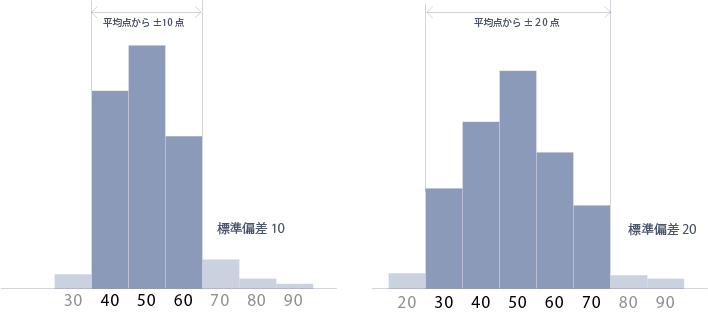
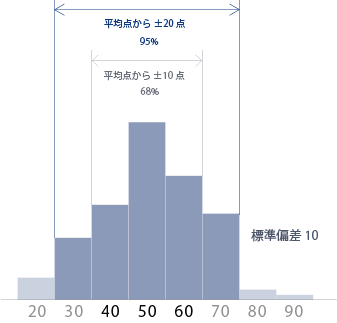
多くの値が標準偏差内に集結する。具体的には、
例えば、平均点が50点のテストがあるとして、その標準偏差が10でした。一般的にはデータの確率分布が正規分布とよばれる形をしていたら、
50点±10点の範囲(40〜60点)にあるデータが含まれる確率が、68%
50点±20点の範囲(30〜70点)にあるデータが含まれる確率が、95%
と言われている。
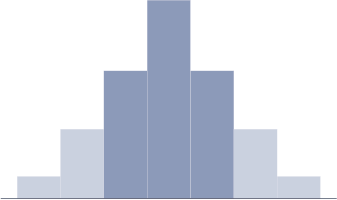
正規分布とは、
「テストの点数の分布図などを作ったときに、平均周辺の値の人数が一番多く平均から離れるにつれてどんどん人数が減っていく傾向にある分布」
のことを言います。ヒストグラムなどで表現した場合に以下のような綺麗な山形になっている状態です。
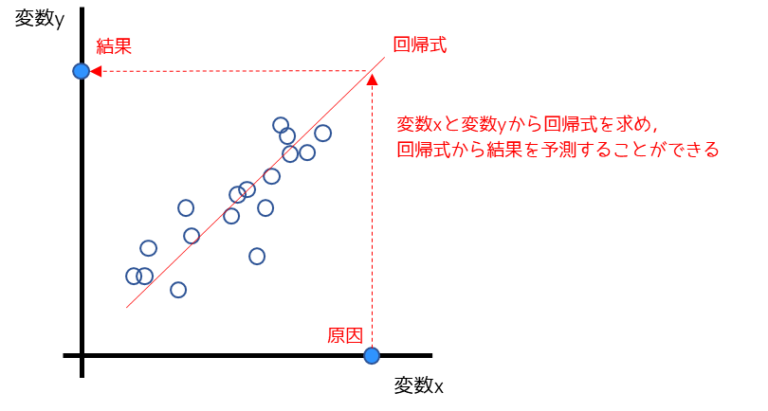
回帰分析
データを分析し項目間の関係を数式をしてモデル化する手法
基本情報では1次式で表す。(例:y = 1.1x + 10)
xに値を代入してyを導く。
2次式で表すときは2次回帰という。